Произведение операций над матрицами
Вы можете производить большинство операций над матрицами так же, как вы оперируете и с нормальными числами. Например, вы можете их складывать или вычитать, соответственно складывая или вычитая каждый из компонентов.
Для примера, рассмотрим сложение двух матриц размерностью 2х3 - матрицы А и матрицы С:

При сложении матриц А и С нужно складывать каждый из элементов m,n. Суммы элементов займут в результирующей матрице сответствующие места:

Мы также можем умножить матрицу на скаляр k. Например, чтобы умножить матрицу А на 3, мы должны умножить на 3 каждый ее элемент:

Теперь поговорим об умножении двух матриц. Эта операция немного отличается от умножения на скалярную величину. Вы должны запомнить несколько правил:
§
Количество столбцов в первой матрице (n) должно быть равно количеству строк во второй (также n). Это значит, что если размерность первой матрицы (mxn), то размерность второй матрицы должна быть (nхr). Два остальных измерения m и r могут быть любыми;
§ Произведение матриц не коммутативно, то есть А х В не равно В х А.
Умножение матрицы mxn на матрицу nхr может быть описано алгоритмически следующим образом:
1. Для каждой строки первой матрицы:
§ Умножить строку на столбец другой матрицы поэлементно.
§ Сложить полученный результат;
2. Поместить результат в позицию [i,j] результирующей матрицы, где i - это строка первой матрицы, a j - столбец второй матрицы.
Для простоты посмотрим на рисунок 4.9:
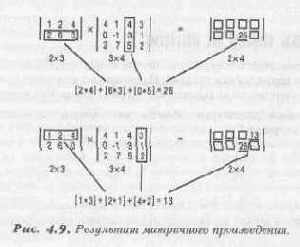
Мы можем это сделать намного проще, написав программу на Си. Давайте определим матрицу 3х3 и напишем функцию, умножающую матрицы. В Листинге 4.9 показана соответствующая программа.
Листинг 4.9. Определение и умножение двух матриц.
// общая структура матрицы
typedef sruct matrix_typ
{
float elem[3][3]; // место для хранения матрицы
} matrix, *matrix_ptr;
void Mat_Mult3X3 (matrix_ptr matrix_1, matrix_ptr matrix_2, matrix_ptr result)
{
index i,j,k;
for(i=0; i<3; i++)
{
for (j=0; j<3; j++)
{
result[i][j] = 0; // Инициализация элемента
for(k=0; k<3; k++)
{
result->elem[i][j]+=matrix_1->elem[i][k] * matrix_2->elem[k][j];
} // конец цикла по k
} // конец цикла по j
} // конец цикла по i
} // конец функции
Перед выходом из этой функции мы имеем результат, сохраненный в переменной result.