Копирование на экран
Создание настоящей трехмерной графической системы — довольно сложное дело. Этому посвящены целые книги (еще толще, чем та, которую вы держите в руках). В первом приближении нам нужны:
§ Кое-какие трехмерные объекты;
§ Объем просмотра;
§ Проекция на план (плоскость) просмотра.
Мы можем быть спокойны относительно трехмерных объектов — мы определили многоугольники как множество вершин и построили на их основе объекты. А вот что касается объема просмотра и плана просмотра, то тут требуются некоторые разъяснения.
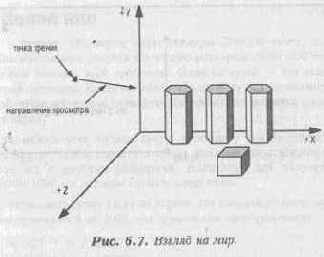
Когда мы смотрим на трехмерный мир, то сами должны в нем где-то находиться и иметь направление просмотра. Рисунок 6.7 иллюстрирует эту мысль.
Учитывая, что в реальном мире мы смотрим на объекты с определенной точки и в определенном направлении, мы можем их построить на экране, который и будет являться планом просмотра. Такой подход довольно сложен, поскольку требует выполнения множества преобразований для решения данной задачи в общем виде. Но, поскольку мы программисты, нас не очень должно волновать общее решение задачи. Нам надо создавать игры, выглядящие как трехмерные.
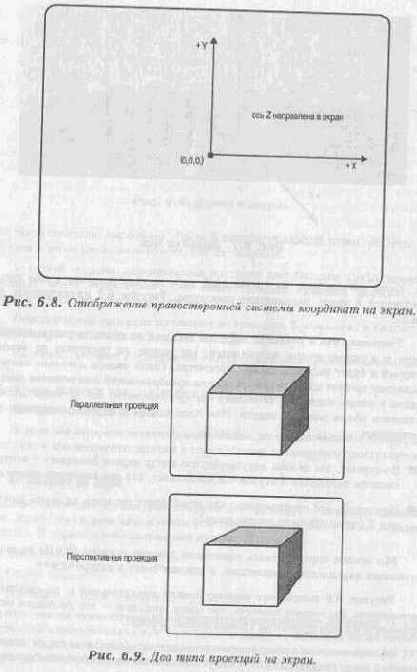
§ Во-первых, мы делаем допущение, что центр экрана совпадает с центром системы координат. Рисунок 6.8 показывает, как она выглядит на экране;
§ Во-вторых, мы предполагаем, что игрок будет смотреть на экран вниз по оси Z (отрицательное направление).
Мы можем спроецировать одиночный пиксель в точку (0,0,0) на экран, используя параллельную проекцию, и увидеть точку в центре экрана. Рисунок 6.9 показывает разницу между параллельной и перспективной проекциями. Вы можете заметить, что центр проекции - это дистанция между игроком и планом просмотра (поверхностью экрана).
Математика для проецирования трехмерных объектов на экран сказочно проста и мы ее реализуем за пару минут. Но пока поговорим о масштабировании.